10 minute read

계량경제 기초 개념들

데이터 분석/모델링을 함에 있어 정말 기초의 기초로 알고 있어야 한다고 생각하는 개념들을 정리해 보았습니다.

데이터의 종류

  • Cross-sectional data (횡단면 자료): 한 시기에 여러 entity를 대상으로 수집한 데이터
    • Heteroskedasticity 와 설명력을 나타내는 $R^2$가 0.4 정도면 잘나온것
  • Time series data (시계열 자료): 한 entity를 대상으로 여러 시간대에 걸쳐 수집한 데이터
    • autocorrelation 과 설명력을 나타내는 $R^2$가 잘나옴 0.7이상
  • Panel data (패널 자료): 고정된 여러 entity를 대상으로 여러 시간대에 걸쳐 수집한 데이터
    • error가 보려고 하는 자료에 따라 one-way, two-way error component를 고려 할 수 있음
    • fixed effects시 자유도 및 $R^2$ 가 잘 안나옴 (within variation 만 이용하기 때문)
    • 횡단면 관측의 시계열을 같이 고려함으로써 좀 더 많은 정보, 큰 변동성, 변수 사이의 낮은 다중공선성, 더 많은 자유도와 효율성을 확보하게됨
    • 순수 횡단면, 시계열 자료에서는 관측할 수 없는 효과를 찾아내고 측정하는 데 우수
    • short panel N이 T보다 많음(짧은 기간 관측) 반대는 long패널

회귀분석의 기초 용어 및 notation

$\mu$ 모평균 $\hat \mu$ 표본평균 (hat이 붙은건 sample을 뜻함)

$\sigma^2$ 모분산 $s^2$표본분산 (편차의 제곱의 평균) 편차란? 관측값에서 평균 또는 중앙값을 뺀것. 즉, 확률변수가 취할 수 있는 가능한 모든 값들이 기대값으로부터 퍼진 정도 (표준편차 = 분산에 루트 씌움)

$u_i$ 모 회귀식의 에러텀
$e_i , \epsilon_i$ 표본 회귀식의 잔차(residual, 오차항 ui의 추정량)

기대값 $E(X)$

  • 대문자는 확률변수 소문자 x는 확률변수의 값으로 통용
  • 확률과정에서 얻을 수 있는 (확률변수가 취할 수 있는) 가능한 모든 값의 가중평균

분산 variance

  • $Var(Y)=E[(Y-E(Y))^2]$
  • Y가 가능한 값의 분포가 얼마나 넓게 퍼져 있는지

공분산 covariance

  • $Cov(X_i,Y_i) = E[(X_i - E(X_i))(Y_i - E(Y_i))]$

  • 기대값(X의 편차 x Y 의 편차)

  • 두개의 확률변수의 선형관계를 나타냄! 한 확률 변수의 증감에 따른 다른 확률 변수의 증감의 경향에 대한 척도

간단한 선형회귀 모형

  • $Y_i = \beta X + u_i \space \text{population regression}$

  • $\beta X = \beta_1 + \beta_2X_{2i} + \dots + \beta_k X_{ki} = E[Y_i \vert X] $

  • $\beta$ 값들은 regression coefficient 또는 regression parameter로 부름 (또는 그냥 beta coef)

OLS 에 의해서 beta coef와 variance 추정

  • 단순 회귀 $\hat \beta = \frac{\sum x_i y_i}{\sum x_{i}^{2}} = \frac{\hat {Cov}(X_i,Y_i)}{\hat {Var}(X_i)}$

  • 다중 회귀(행렬로 표현시) $\hat \beta = (X^\prime X)^{-1}(X^\prime Y)$

    beta coef 유도

    \(Y = X \hat \beta + e\)
    \(e = Y-X \hat \beta\)

    OLS를 적용하면 (잔차의 제곱합을 minimize)

    \[\min \sum^{n} _{i=1} e^2_{i}\]

    \(e^{\prime}e = (Y-X \hat \beta)^{\prime}(Y-X \hat \beta)\)
    \(= Y^{\prime}Y - Y^{\prime}X \hat \beta - \hat \beta X^{\prime} Y + \hat \beta^{\prime} X^{\prime}X \hat \beta\)
    \(= Y^{\prime}Y -2 \hat \beta X^{\prime} Y + \hat \beta^{\prime} X^{\prime}X \hat \beta \ \ \ \because (A^{\prime}B)^{\prime} = B^{\prime}A\)

    극소값의 1계 조건은
    \(\frac{\partial e^{\prime}e}{\partial \hat \beta}\)

    \(= -2 X^{\prime}Y + 2X^{\prime}X \hat \beta = 0\)
    \(= X^{\prime}X \hat \beta = X^{\prime}Y\)
    \(\hat \beta = (X^\prime X)^{-1}(X^\prime Y)\)

    [참고] 회귀분석의 가정 만족시, beta coef 가 unbiased estimator임

    \(\hat \beta = (X^\prime X)^{-1}\)
    \(= (X^\prime X)^{-1} X^\prime (X \beta+u)\)
    \(= (X^\prime X)^{-1} X^\prime X \beta + (X^\prime X)^{-1} X^\prime u\)
    \(= \beta + (X^\prime X)^{-1} X^\prime {u} \space ( \because (X^\prime X)^{-1} X^\prime X = I)\)

    \(E[\hat \beta] = E[\beta] + E[(X^\prime X)^{-1} X^\prime u]\)
    \(= \beta + E[(X^\prime X)^{-1} X^\prime u] \space (\because \beta \text{ is constant that we do not know})\)
    \(\beta + (X^\prime X)^{-1} X^\prime E(u) \space (\because X \text { is non-stochastic by assumption} )\)
    \(= \beta \space (\because \text{ by assumption} \space E(u)=0)\)

  • 단순 회귀 $Var(\hat \beta) = \frac{\sigma^2}{\sum x_i ^2}$

  • 다중 회귀 $Cov(\hat \beta)$ ($\hat \beta 의 $ variance-covariance matrix)

    \[\begin{bmatrix} Var(\hat \beta_1) & Cov(\hat \beta_1 \hat \beta_2) & \cdots & Cov(\hat \beta_1, \hat \beta_k) \\ Cov(\hat \beta_2,\hat \beta_1) & Var(\hat \beta_2) & \cdots & Cov(\hat \beta_2,\hat \beta_k)\\ \vdots & \vdots & \vdots & \vdots \\ Cov(\hat \beta_k, \hat \beta_1) & Cov(\hat \beta_k, \hat \beta_2) & \cdots & Var(\hat \beta_k) \\ \end{bmatrix} =\sigma^2(X^\prime X)^{-1}\]
    variance-covariance 유도
    \[Cov(\hat \beta) = E[[\hat \beta - E(\hat \beta)] \space [\hat \beta - E(\hat \beta)^\prime]]\] \[= E[[\hat \beta - \beta][\hat \beta - \beta]^\prime] \space \because E(\hat \beta) = \beta\] \[= E[[(X^\prime X)^{-1}(X^ \prime) u] [(X^\prime X)^{-1}(X^ \prime) u]^{\prime}] \space (\because \hat \beta = \beta + (X^\prime X)^{-1}(X^ \prime) u )\] \[= E[[(X^\prime X)^{-1}(X^ \prime) u] [u^\prime X (X^\prime X)^{-1}]] \space (\because (AB^\prime) = B^\prime A^\prime)\] \[= E[(X^\prime X)^{-1}(X^ \prime) u u^\prime X (X^\prime X)^{-1}]\] \[= (X^\prime X)^{-1}(X^ \prime) E[u u^\prime] X (X^\prime X)^{-1} \space (\because \text{by assumption X is non-stochastic} )\] \[= (X^\prime X)^{-1}(X^ \prime) \sigma^{2}I X (X^\prime X)^{-1} \space (\because \text{by assumtion } E[uu^\prime] = \sigma^2I )\] \[= \sigma^2 (X^\prime X)^{-1}(X^ \prime X) (X^\prime X)^{-1}\] \[= \sigma^2 (X^\prime X)^{-1}\]

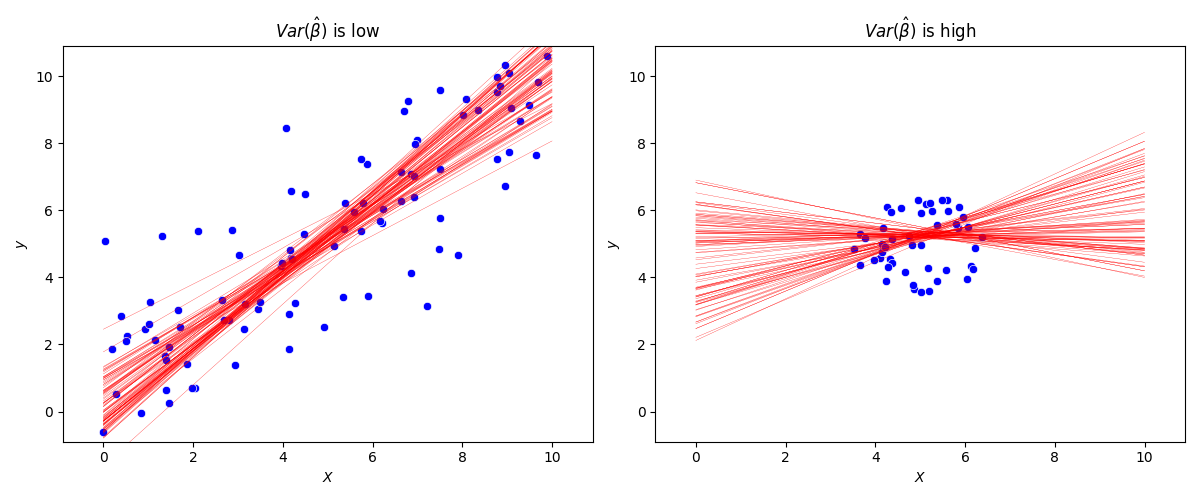
  • sample 수인 n 이 증가하거나 $\hat {Var}(X)$ 가 커지면 $Var(\hat \beta)$는 작아지고, 반대로 n이 감소하거나 $\hat {Var}(X)$ 가 작아지면 $Var(\hat \beta)$는 커진다

code 

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

def create_uniform_data(n_samples=100):
    np.random.seed(1)
    X = np.random.uniform(0, 10, size=n_samples)
    y = X + np.random.normal(0, 2, size=n_samples)
    return X, y

def create_circular_data(n_samples=50, r=1.5):
    t = np.random.uniform(0, 1, size=n_samples)
    u = np.random.uniform(0, 1, size=n_samples)
    X = r * np.sqrt(t) * np.cos(2 * np.pi * u) + 5
    y = r * np.sqrt(t) * np.sin(2 * np.pi * u) + 5
    return X, y

# Create figure and subplots
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

X_uniform, y_uniform = create_uniform_data()
sns.scatterplot(x=X_uniform, y=y_uniform, color=^{\prime}blue^{\prime}, ax=ax1)
ax1.set_title("$Var(\\hat \\beta)$ is low")
ax1.set_xlabel(^{\prime}$X$^{\prime})
ax1.set_ylabel(^{\prime}$y$^{\prime})

X_circular, y_circular = create_circular_data()
sns.scatterplot(x=X_circular, y=y_circular, color=^{\prime}blue^{\prime}, ax=ax2)
ax2.set_title("$Var(\\hat \\beta)$ is high")
ax2.set_xlabel(^{\prime}$X$^{\prime})
ax2.set_ylabel(^{\prime}$y$^{\prime})

# Perform repeated OLS regressions to demonstrate Variance of beta hat
for i in range(100):
    # Uniform data
    temp_t = np.random.randint(50, 101)
    temp_b = temp_t - np.random.randint(10, 25)
    X_sub = X_uniform[temp_b:temp_t].reshape(-1, 1)
    y_sub = y_uniform[temp_b:temp_t]
    model = LinearRegression()
    model.fit(X_sub, y_sub)
    x_line = np.linspace(0, 10, 100)
    y_line = model.predict(x_line.reshape(-1, 1))
    ax1.plot(x_line, y_line, color=^{\prime}red^{\prime}, linewidth=0.2)
    ax1.set_ylim([-0.9, 10.9])
    ax1.set_xlim([-0.9, 10.9])

    # Circular data
    temp_t = np.random.randint(30, 51)
    temp_b = temp_t - np.random.randint(10, 25)
    X_sub = X_circular[temp_b:temp_t].reshape(-1, 1)
    y_sub = y_circular[temp_b:temp_t]
    model = LinearRegression()
    model.fit(X_sub, y_sub)
    x_line = np.linspace(0, 10, 100)
    y_line = model.predict(x_line.reshape(-1, 1))
    ax2.plot(x_line, y_line, color=^{\prime}red^{\prime}, linewidth=0.2)
    ax2.set_ylim([-0.9, 10.9])
    ax2.set_xlim([-0.9, 10.9])

plt.tight_layout()
plt.savefig("example1.png")
plt.show()

회귀분석의 가정

OLS로 추정시의 가정

Unbiasedness Condition

추정량의 기댓값이 그 모수와 같을 조건 $E(\hat \beta_i) = \beta_i$

  • 모형 Linear in parameter: 파라미터를 선형결합 식으로 표현 즉, 독립변수들에 대해 편미분을 하면 상수가 나와야함. 비선형 모델은 예를 들면 $y = \frac{\beta_1x}{\beta_2+x}$

  • 모형 Zero Conditional Mean: $E(e_i \vert X) = E(e_i) = 0$ , 외생성(Exogeneity), 오차항의 기댓값은 독립변수들 X에 상관없이 항상 0 → 에러텀의 기대값이 0이라는것 즉 평균보다 크거나 작은 부분이 상쇄되어 모두 합했을때 그 합이 0 이라는것을 의미
    • 대표본에서 더 약한 가정: $cov(e_i,x_j) = 0$, $i \neq j$
  • 샘플 Random Sampling: i.i.d 조건(independent and identically distributed) 각각의 분포(주변분포)는 모두 같고 모두 독립일 조건.
  • 샘플 No Perfect Multicollinearity: 다중공선성(독립변수들 간의 선형관계=상관정도)이 적거나 없어야함
    • k개의 계수를 추정하려고 하면 k개의 독립된 정보가 필요하기 때문
    • $Rank(X) = k$, rank란 선형독립인 행(또는 열)의 최대수. 즉, 행렬 X의 rank가 k 라는 것은 k개의 열벡터 $X_1,X_2,…,X_k$가 서로 선형독립이라는 의미

Efficiency Condition

오차항에 대한것, 가장 분산이 작을 조건(분산이 더 작을 수록 더 정확하다), $Var(\hat \beta_i) \leq Var(\tilde \beta)$

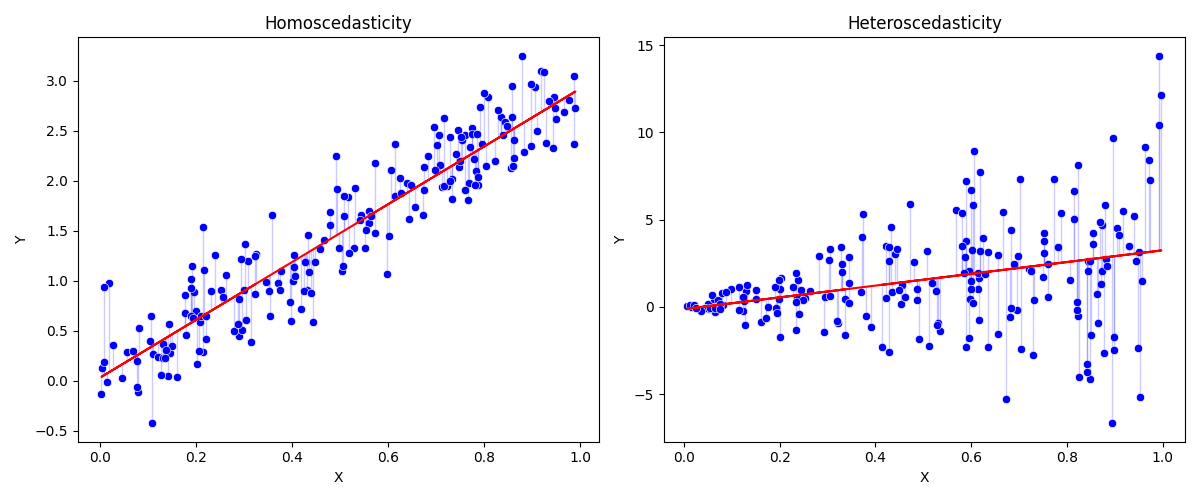
  • Homoscedasticity(오차항의 동분산): $Var(u_i\vert X) = Var(u_i) = E(e_i^2) = \sigma^2$
    • X가 어떤 값을 가지든 모든 i에 대하여 u의 분포는 똑같다는것.
      • 소득이 100만원인 사람의 평균소비가 80 +- 25만원 이고, 소득 120만원 이여도 +-25만원 … → 물론 현실에선 이분산이 더 많을거임
    • 물론 추론에는 표본 잔차인 ei를 이용하지만 이가정은 모집단 ui 에 대한 가정임을 상기하자
    code 
      import numpy as np
  import pandas as pd
  import seaborn as sns
  import matplotlib.pyplot as plt

  def create_data(N=200, heteroscedastic=False):
      data = pd.DataFrame({'X': np.random.uniform(size=N)})

      if heteroscedastic:
          data['Y'] = 3 * data['X'] + np.random.normal(scale=5 * data['X'])
      else:
          data['Y'] = 3 * data['X'] + np.random.normal(scale=0.3, size=N)
      return data

  # Create homoscedastic and heteroscedastic data
  homo_data = create_data()
  hetero_data = create_data(heteroscedastic=True)

  # Create a figure and axis
  fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))

  # Plot homoscedastic data
  sns.scatterplot(x='X', y='Y', data=homo_data, ax=ax1, color='blue')
  ax1.set_title('Homoscedasticity')

  # Plot the lines from data points to the regression line
  coefs_homo = np.polyfit(homo_data['X'], homo_data['Y'], 1)
  y_fit_homo = coefs_homo[0] * homo_data['X'] + coefs_homo[1]
  for i in range(len(homo_data)):
      ax1.plot([homo_data['X'][i], homo_data['X'][i]], [homo_data['Y'][i], y_fit_homo[i]], color='blue', alpha=0.2, lw=1)

  # Change or add regression line from regplot
  ax1.plot(homo_data['X'], y_fit_homo, color='red', label='Regression Line')

  # Plot heteroscedastic data
  sns.scatterplot(x='X', y='Y', data=hetero_data, ax=ax2, color='blue')
  ax2.set_title('Heteroscedasticity')

  # Plot the lines from data points to the regression line
  coefs_hetero = np.polyfit(hetero_data['X'], hetero_data['Y'], 1)
  y_fit_hetero = coefs_hetero[0] * hetero_data['X'] + coefs_hetero[1]
  for i in range(len(hetero_data)):
      ax2.plot([hetero_data['X'][i], hetero_data['X'][i]], [hetero_data['Y'][i], y_fit_hetero[i]], color='blue', alpha=0.2, lw=1)

  # Change or add regression line from regplot
  ax2.plot(hetero_data['X'], y_fit_hetero, color='red', label='Regression Line')

  plt.tight_layout()
  plt.savefig("example2.png")
  plt.show()

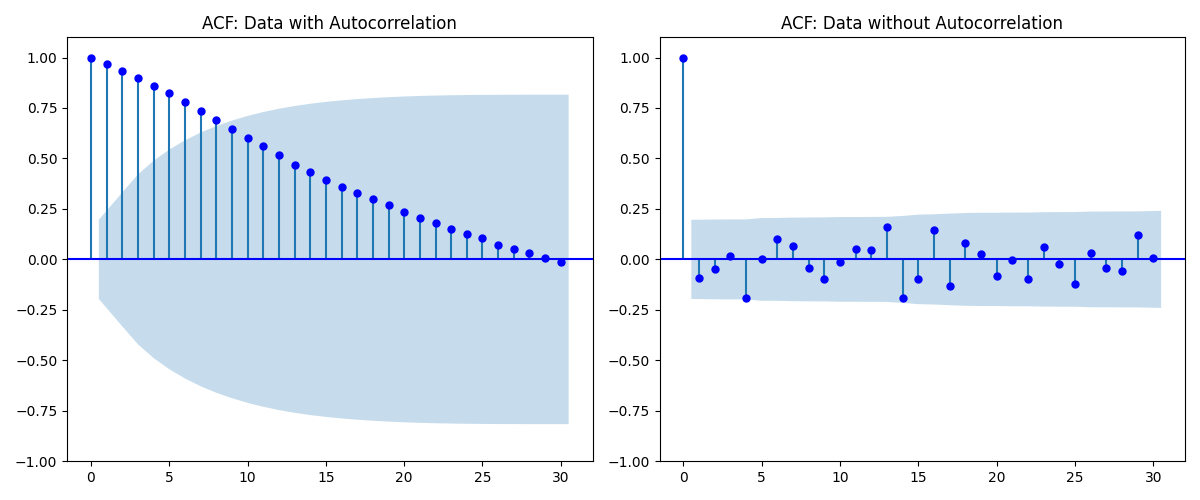
  • No Autocorrelation(자기상관 없음): $cov(u_i,u_j) = E(e_i \cdot e_j) = 0$, $i \neq j$ 자기상관 있음 = 트렌드있음 이라 생각하면 편함

    code 
      import numpy as np
  import pandas as pd
  import matplotlib.pyplot as plt
  import statsmodels.api as sm

  np.random.seed(42)

  def create_data(n=100, autocorr=False, ar=[0.5,-0.5], sigma = 0.2):
      if autocorr:
          ar_process = sm.tsa.ArmaProcess(ar=ar)
          data = ar_process.generate_sample(n, scale = sigma)
      else:
          data = np.random.normal(0, sigma, n)
      return pd.Series(data)

  # Create data with and without autocorrelation
  data_autocorr = create_data(autocorr=True)
  data_no_autocorr = create_data()

  # Plot ACF
  fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
  sm.graphics.tsa.plot_acf(data_autocorr, lags=30, ax=ax1, title='ACF: Data with Autocorrelation', color="blue")
  sm.graphics.tsa.plot_acf(data_no_autocorr, lags=30, ax=ax2, title='ACF: Data without Autocorrelation', color="blue")
  ax1.set_ylim([-1, 1.1])
  ax2.set_ylim([-1, 1.1])
  plt.tight_layout()
  plt.savefig("example3.png")
  plt.show()

    </div>

    </details>

행렬로 표현시 Homoscedascity 와 no Autocorrelation 은 한번에 표현이 가능함

\[e = \begin{bmatrix} e_1 \\ e_2 \\ \vdots \\ e_n \end{bmatrix}\] \[ee\prime =\begin{bmatrix} e_1 \\ e_2 \\ \vdots \\ e_n \end{bmatrix} \begin{bmatrix} e_1 & e_2 & \cdots & e_n \end{bmatrix} = \begin{bmatrix}e_1e_1 & e_1e_2 & \cdots & e_1e_n \\ e_2e_1 & e_2e_2 & \cdots & e_2e_n \\ \vdots & \vdots & \vdots & \vdots \\ e_ne_1 & e_ne_2 & \cdots & e_ne_n \\ \end{bmatrix} = \begin{bmatrix}e_1^2 & e_1e_2 & \cdots & e_1e_n \\ e_2e_1 & e_2^2 & \cdots & e_2e_n \\ \vdots & \vdots & \vdots & \vdots \\ e_ne_1 & e_ne_2 & \cdots & e_n^2 \\ \end{bmatrix}\] \[E(ee\prime) = \begin{bmatrix} E(e_1^2) & E(e_1e_2) & \cdots & E(e_1e_n) \\ E(e_2e_1) & E(e_2^2) & \cdots & E(e_2e_n) \\ \vdots & \vdots & \vdots & \vdots \\ E(e_ne_1) & E(e_ne_2) & \cdots & E(e_n^2) \\ \end{bmatrix} = \sigma^2I_n\]

(가정에 의해 $E(e_i^2) = \sigma^2$ $E(e_i \cdot e_j) = 0$, $i \neq j$ 이므로 , $I$는 항등행렬)

Dummy Variable (더미변수)

독립변수의 categorical variable을 더미 변수로 변환하면 분석이 가능함.

  • Different intercept, Same slope : $Y_i = \beta_0+\beta_1 X_i + \beta_2 D_i + u_i$
    • $\beta_2$가 더미변수의 coef 해석은 간단함 0 보다 1일때의 차이
  • 더미변수란 binary로 0 과 1 값만 가지는 변수 (ex 남자면 1 여자면 0)을 뜻하며, 회귀분석을 할시 categorical variable을 여러개의(number of category - 1 ) 더미 변수로 만들어 통제해 사용한다.
  • 더미변수는 추정치를 바꾸지 않고 절편만을 바꾸어 평행하게 움직이는 역할이라 생각하면 된다.
  • 0 의 값을 갖는 범주는 reference, benchmark, baseline 등으로 부르며 비교군이 됨
  • 더미변수가 여러개라면 reference group의 의미를 파악해야 해석하기 쉬움
  • 더미변수는 로그를 취할 수 없음 (1, 0.0001 또는 np.log1p() 등을 통해 로그 취할순 있음!)
  • 각 더미계수는 1개의 자유도를 감소시킴 → 표본 크기가 작으면 많은 더미변수 포함 못함
    • 회귀분석에서 자유도란? observation 수 - 추정할 독립변수의 수 빼기
    • 표본크기가 작으면 패널분석시 fixed effect 하기 어려울 수 있음
  • 구조적 변화에 있어서도 더미변수 활용 함 → 이벤트 전후, 이벤트 여부, 분기별 더미, 계절더미 등으로 계절요인제거 deseasonalization 이 가능

Interaction Term (상호 작용항)

한 독립변수의 변화가 또다른 독립변수의 종속변수 y에 대한 영향력을 어떻게 변경 하는지 알아보기 위해서 사용

상호작용이 있을 경우, 각각의 변수의 Coefficient는 의미가 없을 수도 있음

  • 두 개의 Binary 변수사이에 상호작용
    • 두 개의 Binary 변수를 $D_1(성별), D_2(학력)$ 라고 하고 임금에 대해서 회귀 분석을 한다고 해보자면,
    • $Wage_i = \beta_0 + \beta_1 D_{1i} + \beta_2 D_{2i} + \beta_3 (D_{1i}D_{2i}) + u_i$로 표현 할 수 있으며 $\beta_3$ 가 성별에 따른 학력 수준 영향력의 차이를 보여줌.
      (두 집단 남여 의 교육 임금의 차이 - 두 집단 간 기울기의 차이)
  • 하나의 Binary 변수와 하나의 Continuous 변수사이에 상호작용
    • Different intercept, Different slope: $Y_i = \beta_0+\beta_1 X_i + \beta_2 D_i +\beta_3(X_i D_i)+ u_i$
    • $\beta_3$는 더미가 1일때 Continuous 변수가 한단위 증가할때의 y 가 얼마나 변하냐를 뜻함

회귀분석에서 변수의 단위 계수 해석

독립변수의 단위 변환 시 회귀계수의 변화

  • 독립변수에 a를 곱하고 다시 회귀하면 OLS추정치는 1/a 만큼 줄어듬
  • 독립변수에 a를 더하고 다시 회귀해도 OLS추정치는 일정함

종속변수의 단위 변환시 회귀계수의 변화

  • 종속변수에 a를 곱하고 다시 회귀하면 OLS추정치는 a배 증가
  • 종속변수에 a를 더하고 다시 회귀해도 OLS추정치는 일정

Log 변환

Python 에서 로그변환시 변수에 0이 포함된다면, np.log1p() 로 변환하는것이 좋다.

log-level model 해석

$\log y = \alpha + \beta x$

  • $\beta$ 는 $x$ 의 한 단위 변화에 대한 $y$ 의 변화율. i.e. x 한단위 변화에 따른 y의 퍼센트 변화율($\beta$ x100) 이라 해석
    • 단 더미변수는 $(e^\beta - 1) 100$ 을 변화율로 따져야함 (np.exp(beta) - 1) * 100
  • ln(income) = a + 0.0159 age
    • 나이가 1세 증가함에 따라 소득은 약 1.59% 증가한다
  • ln(income) = a + 0.1148 gender
    • gender가 1일때 $e^{0.1148} \simeq 1.12$ , 즉 gender 가 1인 경우 약 12% 정도 소득이 높다.

level-log model 해석

$y = \alpha +\beta \log x$

  • $x$가 1% 만큼 증가할 때 $y$는 $\frac{\beta}{100}$ 만큼 변화
  • sales = a + 1234log(adv)
    • 광고비가 1% 증가할 때, 매출액은 약 1234원 증가한다

log-log model 해석

$\log y = \alpha + \beta \log x$

  • $x$%변화율에 대한 $y$의 %변화율
  • ln(sales) = a + 0.413log(adv)
    • 광고비가 1% 증가할 때, 매출액은 약 0.4% 증가한다

You may also enjoy

[Econometrics] Econometrics in Python

5 minute read

파이썬에서 계량분석에 대해 어떤 기본적인 라이브러리가 있고, 어떻게 쓰면 되는지 간단한 팁들을 작성해보려 합니다. Patsy: 데이터 전처리와 같은 작업 Statsmodels: 횡단면 및 시계열 데이터 분석 Linearmodels: 패널데이터 분석 Stargazer...